Einleitung
Auf der Suche nach einer Hilfestellung bzgl. einer Rechenaufgabe zum Rentenbarwert ist Daniela über meine Webseite gestolpert. Richtig fündig wurde sie wohl auch dort nicht, denn sie hat die Aufgabenstellung im Gästebuch hinterlassen. In diesem Beitrag möchte ich mich nun an die Lösung heranwagen.Die Aufgabenstellung
Der Vereinfachung halber zitiere ich erstmal aus dem Gästebucheintrag:Eine Lebensversicherung enthält folgende Klauseln für die Kapitalrückzahlung im Erlebnisfall:
-12x eine jährliche Rente i.H. von 20.000€, erstmals bei Vollendung des 60. Lebensjahres
-Ablösung der VS in einem Betrag bei Vollendung des 60.Lebensjahres
======
Aufgabenstellung: 1.)Berechnen Sie die Ablösesumme unter Zugrundelegung von 5,5 Zinseszins!
2.)Ein Versicherungsnehmer möchte jährlich nur 15.000 € beziehen. Wie oft kann der volle Betrag ausgezahlt werden?
Mein Problem ist Aufgabe 2.
Ich habe bis jetzt den Rentenbarwert berechnet. Jetzt müsste ich nach n ( Laufzeit) umstellen.....
Gut. Also geht es darum aus der Rentenbarwert-Formel die Laufzeit-Formel zu forme(l)n.
Das hier ist die Ausgangsbasis:
Und hier wollen wir hin:
Umformung der Rentenbarwert-Formel: Auflösung nach n
"Sx" ist gleichbedeutend mit "Schritt x". Es folgt die Schrittfolge:Et voilá: Die Formel bei S10 entspricht dem Ziel wie oben vorgegeben.
Die Rechnung
Ich muss gestehen, an der Stelle bin ich ein wenig faul. Ich benutze einfach meinen Rentenbarwert- und meinen Laufzeit-Rechner und gebe dort die Eckdaten ein.Für Aufgabe 1 komme ich auf einen Rentenbarwert von 181.850,73 €
Für Aufgabe 2 (nur 15.000 € jährliche Rente statt 20.000 €) komme ich auf 18 Jahre und eine Restzahlung.
Und die Restzahlung - also im Jahr 19 - beträgt laut meinem Schlussraten-Rechner 10.175,48 €.
Schlussbemerkung
Die mathematische Umformung der Rentenbarwert-Formel ist für Nebenher-Mathematiker wie mich nicht ganz einfach. Zumal wenn man die Anwendung der Logarithmus-Regeln nochmal nachschlagen muss.Die Werte ermitteln ist recht einfach mit entsprechenden Rechenprogrammen - bzw. erfordert etwas Konzentration bei der Eingabe in den Taschenrechner. Ich hoffe, dieser Beitrag hilft dem ein oder anderen - oder regt dazu an, meine Ausführungen nochmals zu überprüfen. Gerade bei meinen Rechenprogrammen gebe ich keine Gewähr - habe ja schließlich schonmal einem Fehler nachspüren dürfen. Oder ist gerade das, das Qualitätsmerkmal?!? Entscheidet selbst!
Ich freue mich auf jeden Fall immer über Feedback. Sei es Kritik, Lob - oder auch mal eine Frage wie die von Daniela oben. :-)
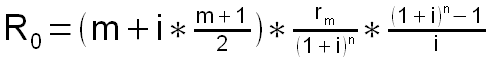
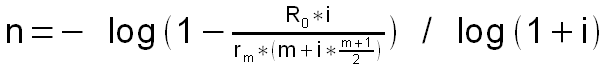

Keine Kommentare:
Kommentar veröffentlichen